Acesso ao Grupo Exclusivo de Telegram e aos cursos MF EXPERT => Click aqui

 

Introdução Artigo

 

Vamos aprender agora como calcular um portfólio ótimo usando o modelo de Markowitz . Para isso, vamos aprender também como usa o solver no Excel.

INTRODUÇÃO

 

Já aprendemos o caso com dois ativos.

Agora vai ficar mais claro o conceito de otimização de portfólio quando temos mais opções de ativos para escolher.

Responderíamos às perguntas:

• “Eu quero um portfólio com um retorno esperado de 10%. Qual seria o melhor peso para se colocar em cada ativo?”

Nesse caso, eu estaria respondendo à pergunta sobre qual combinação teria um retorno de 10%, com a menor volatilidade possível.

Ou também,

• “Eu quero um portfólio com uma volatilidade de, no máximo, 8%. Qual seria o melhor peso para se colocar em cada ativo?”

Aqui, eu estaria respondendo à pergunta sobre qual combinação teria uma volatilidade de 8% e o maior retorno possível.

Essas perguntas se respondem, plotando a fronteira eficiente que já explicamos aqui.

Mas, no caso com 2 ativos, é um pouco mais tranquilo, principalmente porque é fácil criar “na mão” todas as combinações possíveis entre eles.

 

OTIMIZAÇÃO DE PORTFÓLIO

 

Para construir esse problema, precisamos estimar 3 informações: o retorno esperado de cada ativo, a volatilidade e a matriz de correlação.

Mais uma vez, você precisa entender a matemática de portfólio, agora o caso com N ativos.

Com essas 3 informações estimadas e o peso para cada ativo, conseguimos calcular o retorno esperado do portfólio e sua volatilidade.

O que precisamos agora é resolver um problema de otimização linear.

As fórmulas são um pouco complicadas, mas o Excel já tem uma ferramenta que faz esse trabalho para você – o Solver!

O Solver do Excel não vem instalado automaticamente, mas é bem simples configurar. Olha esse link aqui.

Antes de entender o Solver, vamos entender o Set up inicial.

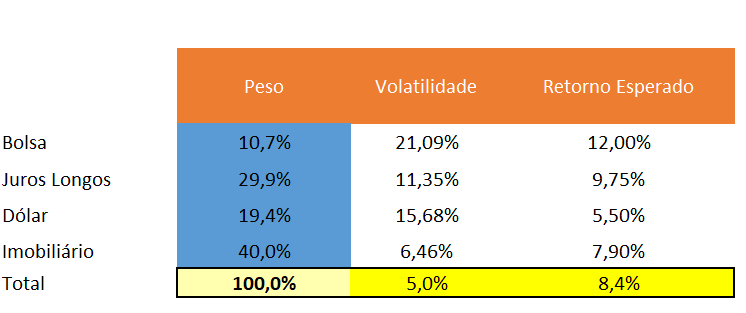
Supondo que temos esses 4 ativos para montar o portfólio, estimamos, então, seus respectivos retornos esperados, volatilidades e matriz de correlação.

 

 

Agora, vamos supor que queremos o melhor portfólio possível, mas respeitando que a volatilidade não seja maior do que 5%.

No Excel está montado dessa forma. Os dados estimados em branco e em amarelo estamos calculando a volatilidade total no portfólio e o valor esperado, dado um peso para cada ativo.

Esse peso pode começar em qualquer valor. Note que a Vol calculada ainda não está igual ao objetivo de volatilidade do problema.

 

SOLVER

 

Agora vamos entender como funciona o SOLVER.

O solver é uma ferramenta do Excel para resolver problemas que não seriam resolvidos via uma única fórmula.

Explicando de maneira simplificada, no exemplo anterior, na prática seria como se o SOLVER ficasse mudando os pesos dos ativos (em azul) para testar as milhares de combinações possíveis.

Assim, ele conseguiria achar qual portfólio com uma volatilidade de 5% teria o maior retorno esperado.

É claro que ele não testa todas as combinações possíveis, pois elas aumentariam exponencialmente como o número de ativos. O SOLVER faz isso de maneira ótima, sempre tentando convergir para a solução.

O que você precisa aprender agora é como configurar esse problema de otimização.

O solver normalmente você acha la no canto direito na aba “Data” do Excel.

 

O SOLVER funciona da seguinte forma:

Você tem que definir a célula que quer maximizar ou minimizar.

No exemplo, como estamos travando a volatilidade, queremos maximizar o retorno esperado. Então, coloquei como objetivo maximizar a celula E11 (onde estou calculando o valor esperado do Portfólio)

 

Depois indicamos em quais células o SOLVER vai poder mexer para tentar achar a solução. Então, perceba que nesse campo, está selecionado o range em que estão os pesos dos ativos no portfólio  (Células C7:C10)

 

 

 

 

E, por último, definimos algumas restrições que queremos.

 

 

 

 

 

 

 

 

 

 

 

A primeira: a volatilidade do portfólio deve ser igual à volatilidade target. (D11=E14)

A segunda: o peso das ações deve somar 100%. Ou seja, o portfólio não deve ficar como caixa (C11=1)

E, por último, o peso das ações deve ser maior que zero (sem short sell). (C7:C10>0)

A primeira restrição é obrigatória, mas as outras vão depender das restrições específicas do portfólio.

Podem-se colocar mais restrições, como por exemplo, que uma ação não pode passar de 30% do total.

Agora, é só rodar o SOLVER, para ele achar uma solução. Na planilha para Download essa estrutura do SOLVER já está montada.

Portanto, o Portfólio a seguir é o melhor portfólio que conseguimos montar com uma Vol de 5%

 

Lembrando que, em alguns casos, o Solver não vai achar uma solução. Como por exemplo, escolher uma volatilidade impossível de se alcançar (uma volatilidade abaixo da volatilidade do Portfólio de mínima variância.

 

FRONTEIRA EFICIENTE COM N ATIVOS

 

Agora como ploto aquela fronteira eficiente para esse portfólio com vários ativos.

Como ficaria inviável testar todas as combinações possíveis. Temos que pensar outra forma de fazer, e para isso vamos usar o SOLVER.

É fácil achar o portfólio de mínima variância com esses ativos. Seria um problema de minimização da célula onde calculo a volatilidade.

E o mesmo para achar qual seria a volatilidade máxima. Nesse caso seria um problema de maximizar a célula onde calculo a volatilidade.

Agora partindo dessa volatilidade mínima até a máxima com um passo que eu defino (usei 0,5%), vou calculando qual seria o portfólio com o maior retorno esperado.

Fazendo isso estamos plotando a fronteira eficiente.

Em laranja é essa fronteira. Em vermelho destaquei “Portfólios” 100% investidos em cada classe de ativo que não estão dentro da fronteira.

É importante lembrar, que posso gerar qualquer combinação de portfólio que quiser que nunca estará em um ponto acima da fronteira eficiente.

Por exemplo, com a volatilidade dos Juros Longos, eu consigo gerar um portfólio com maior retorno esperado, combinando os ativos.

Por isso, os portfólios que estão na fronteira eficiente, são conhecidos como portfólios eficientes.

 

RESTRIÇÕES

 

Eu sei que parece muito legal e que você vai querer sair aplicando esse modelo no seu portfólio. Mas é importante entender algumas limitações.

Você deve entender que essa otimização de portfólio está assumindo que o modelo tem em mãos boas estimativas.

A volatilidade conseguimos estimar com alguma precisão. No entanto, nas correlações já aparecem algumas limitações, mas o problema mesmo está na estimativa de retorno esperado.

Começando com o problema da correlação, é importante entender que as correlações não são constantes no tempo.

Existe até uma máxima do mercado financeiro que diz que, na crise, as correlações vão todas para 1. Isso quer dizer que todos os ativos vão cair juntos.

Então, às vezes, pode dar impressão que se estaria montando um portfólio otimizado e diversificado, quando, na prática, isso não é verdadeiro.

No retorno estimado, as estimativas perdem ainda mais a precisão. É difícil fazer boas previsões de retorno estimado pois o modelo de otimização está assumindo que aquele é o real retorno esperado do ativo.

Depois, faça o teste…

Altere um pouco o valor esperado dos ativos e perceba como vai produzir portfólios completamente diferentes.

Por isso, se diz que não é um modelo muito estável.

O pior ainda são os livros e as aulas que usam o retorno passado, tipo uma média do retorno passado, como estimativa de valor esperado futuro.

Pense só no que se está assumindo ao fazer isso: ativos que foram bem no passado vão continuar indo bem, e os que foram mal vão continuar indo mal.

E a gente sabe que retorno passado não é garantia de retorno futuro!

Então, usar essa otimização de portfólio com esse tipo de estimativa, não recomendo nem um pouco fazer.

O que eu faço, às vezes, para tentar estimar esse valor esperado, é criar cenários e atribuir probabilidades e retornos a eles:

 

 

Assim, o modelo vai funcionar se a sua capacidade de estimar valores esperados for boa. Por que já sabemos que utilizar os retornos passados para isso não é uma boa ideia.

 

CONCLUSÃO

 

Para concluir, por mais que eu ache que você não deve usar o modelo cegamente para montar um portfólio, acredito que pode ser usado, pelo menos, para verificar algumas inconsistências no seu portfólio.

Do tipo, vamos supor que você tenha 5% do ativo A, e a alocação ótima para ele é 20%.

Isso ia fazer refletir, se dado o risco/retorno que você está enxergando para esse ativo, se não seria uma boa ideia aumentar sua a posição.

Mas você deve entender todas as limitações do modelo, e entender que ele não é tão “mágico” quanto parece.

O modelo é um bom começo para começar a pensar em diversificação e comparação de risco/retorno dos ativos.

 

Planilha para Download