Acesso ao Grupo Exclusivo de Telegram e aos cursos MF EXPERT => Click aqui

 

Introdução Artigo

 

No artigo de hoje, vamos entender uma das medidas de risco mais usadas no mercado, o Value-at-Risk. E, é claro, vamos ver como é simples calculá-la no Excel.

Se prepara… Será um artigo bem extenso, mas é quase uma aula de risco de mercado completa!

 

Introdução

 

Já falamos da volatilidade como métrica e como medida de risco. E do máximo drawdown também.

Agora, vamos abordar o Value-at-Risk ou simplemente VaR.

Essa é uma das medidas mais utilizadas por fundos de investimento e por grandes bancos. Muita gente, até do mercado financeiro, nunca parou para tentar entendê-la pois acha que é algo muito complicado.

Mas não é!

Antes de aprendermos a calculá-la, é muito importante entender a intuição por trás dela.

A definição de que mais gosto é:

O Value-at-Risk representa a perda máxima potencial de uma carteira ou ativo, em um horizonte de tempo definido, com um determinado grau de confiança.

Note que há 3 parâmetros em destaque: horizonte de tempo; perda máxima; e grau de confiança.

Falar que o VaR de PETR3 = -6% não significa absolutamente nada!

Para fazer sentido, você deve especificar os 3 parâmetros.  No caso anterior, o -6% seria a perda máxima. Está faltando definir para qual horizonte de tempo essa perda máxima se refere e com que grau de confiança.

O grau de confiança é a probabilidade que está associada à medida. Ela pode ser expressa por um número alto, 95% ou 99%, por exemplo. Ou por um número baixo, como 5% ou 1%.

Mas, independente do padrão escolhido, a interpretação é exatamente a mesma!

Vamos colocar em um exemplo para que fique mais claro…

O que a informação acima quer dizer?

Primeiro, a perda máxima é igual a -4%.

Depois, essa é a perda máxima para um horizonte de 5 dias.

E, por último, se você escolher o padrão 1, você pode interpretar:

Há 95% de chance de, depois de 5 dias, o ITUB3 não cair mais do que 4%.

Já no padrão 2:

Há 5% de chance de, depois de 5 dias, o ITUB3 cair mais do que 4%.

Se parar para pensar, eles significam absolutamente a mesma coisa!!

Vou utilizar aqui o padrão 1, o que considero o mais comum no mercado financeiro.

No exemplo anterior, imagina que o meu patrimônio é de R$100.000 reais em ITUB3 no d0. No dia d+5, qual a chance de o meu patrimônio estar maior que 96.0000?

95% né!

A perda máxima com 95% de confiança é de 4%. Então, se tenho 100 mil, uma perda de 4% é igual a 4000 reais.

Em vez de em termos percentuais, o VaR pode ser expresso em termos financeiros também. Mais um exemplo para fixar:

Quando não indicamos o horizonte de tempo, por padrão, devemos considerá-lo um dia.

Nesse caso, então, podemos falar que há 99% de chance de, depois de 1 dia, eu não perder mais do que R$300.000. com ITUB4

Ou

Há 1% de chance de, depois de 1 dia, eu perder mais do que R$300.000.

É bem simples converter do financeiro para o percentual.

No exemplo anterior, se a posição total de ITUB4 for de R$6.000.000, o VaR, com 99% de confiança, será igual a -5% ( 300k / 6 Milhões)

A lógica inversa também funciona, se o VaR estiver indicando -3% e o tamanho da posição total for de R$10Milhões. O VaR em financeiro será R$10milhões*-3% = R$300.000.

Pronto, entendemos a intuição do VaR agora!

O mais importante é que o VaR é uma medida associada a uma probabilidade.

Se você calculou o VaR, com 99% de confiança, igual a -5%, e o seu ativo caiu mais do que 5%, não quer dizer que a sua medida está “quebrada”.

Temos que lembrar que sempre há uma probabilidade de exceder essa perda máxima.

 

Como calcular?

 

Aprendemos a intuição do Value at Risk, agora temos que aprender como calculá-lo.

Muita gente me pergunta de onde vem os 99% de confiança e o horizonte de tempo.

É importante entender que esses são parâmetros que você escolhe.

O que devemos fazer é calcular a perda máxima, dados esses parâmetros.

Antes de entrar nos métodos, vamos pensar também na intuição do cálculo.

Se quisermos o VaR diário com o 99% confiança, precisamos achar o retorno diário que qualquer retorno abaixo dele ocorra em 1% das vezes e qualquer retorno acima ocorra em 99% das vezes.

Para fazer isso, existem dois métodos:

• Histórico
• Paramétrico

 

MÉTODO HISTÓRICO

 

Vamos pensar na distribuição empíricas dos dados.

Para calcular o VaR, sempre precisamos definir quantos dados vamos utilizar para estimar essa medida.

Vamos supor que utilizaremos os últimos 1000 retornos diários.

Agora, se pegarmos esses retornos e ordenarmos do menor retorno (posição 1) para o maior retorno (posição 1000):

 

 

Repara que o retorno na posição 11 (-7,20%) é o ponto onde eu tenho 1% dos retornos menores que ele e 99% dos retornos maiores.

Se parar para pensar, essa é a definição do VaR com 99% de confiança.

Se quisermos calcular o VaR com 95% de confiança, por exemplo?

Precisamos achar o retorno que, dentro da distribuição, apenas 5% dos retornos são menores que ele e 95% dos retornos são maiores que eles.

Como no caso anterior, a distribuição está ordenada, por isso sabemos que a posição 51 é esse ponto.

Mas, agora como calcular utilizando o Excel?

É claro que não vamos fazer esses passos: ordenar manualmente a distribuição e achar o ponto correspondente ao VaR.

O Excel tem uma fórmula que faz isso para a gente: a fórmula PERCENTILE.

Antes de entrar na fórmula, vamos lembrar da mediana (MEDIAN no Excel) que já vimos lá no colégio.

O que é a mediana?

É o ponto que define a metade de uma distribuição, ou seja, temos 50% da distribuição de um lado e 50% do outro.

O percentil 50% é exatamente a mediana.

Já o percentil 10% é o ponto onde temos 10% da distribuição para um lado e 90% para o outro.

Já deu para perceber que o percentil 5% é exatamente a definição do VaR, com 95% de confiança.

Na fórmula PERCENTILE:

Você só precisa passar o range dos dados (array), no caso a distribuição de retorno, e definir qual o percentil desejado que ela retorne (k).

Portanto, para calcular o VaR pelo método histórico no Excel, só precisamos seguir estes passos:

1. Escolher o tamanho da amostra
2. Calcular os retornos na frequência desejada de horizonte de tempo
3. Consultar o percentil da distribuição empírica

 

MÉTODO PARAMÉTRICO

 

Agora, vamos ver a outra forma de calcular o VaR, utilizando o método Paramétrico.

O método paramétrico tem esse nome, pois, para calcular o VaR, só precisamos consultar os parâmetros de uma distribuição.

O primeiro passo é definir qual distribuição vamos utilizar, ou seja, em qual distribuição encaixaremos os nossos retornos.

As mais usadas são as:

1.  Distribuição Normal
2.  Distribuição T-Student

No entanto, não quer dizer que são as melhores. A popularidade delas está ligada ao fato de serem de mais simples utilização.

Quem tiver curiosidade, pesquise sobre o Extreme Value Theory (EVT) que emprega o uso de distribuições mais complexas para o cálculo do VaR.

Mas, voltando ao método…

Vamos utilizar como exemplo a Distribuição Normal.

A Distribuição Normal conta com apenas 2 parâmetros: média e desvio padrão.

Com esses parâmetros estimados, é tudo que precisamos para conseguir plotar a distribuição. Já até ensinei como plota uma distribuição Normal no Excel.

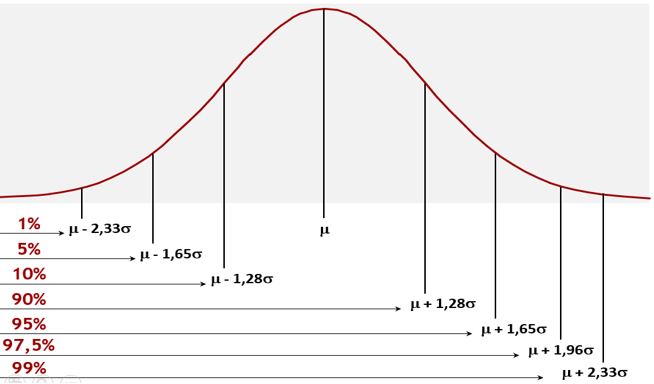
E por ser uma distribuição conhecida, sabemos algumas propriedades. Observe o gráfico abaixo:

 

 

O conseguimos observar?

Se partimos da média e andarmos 1,28 desvio padrão para esquerda, estaremos em um ponto onde temos 10% da distribuição de um lado e 90% da distribuição do outro.

Já se andarmos 2,33 desvios, estaremos em um ponto onde temos 1% da distribuição para um lado e 99% da distribuição para o outro.

Por exemplo, calculamos a média da distribuição igual a 0,5% e o desvio padrão em 1%.

Agora, se fizermos então, 0,5% (média) – 2,33 * 1% (desvio padrão)= -1,83%

Sabemos que valores menores do que -1,83% ocorrem em 1% das vezes em uma distribuição normal (com média 0,5% e desvio padrão 1%) e valores maiores do que -1,83% ocorrem em 99% das vezes.

Ihh essa não é a definição de VaR com 99% de confiança?

Exatamente!

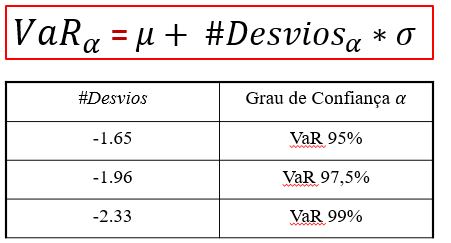
Então, para calcular o VaR pelo método paramétrico com a distribuição normal, devemos, primeiramente, estimar a média e o desvio padrão.

Aí, partindo média, andamos para a esquerda o número de desvios padrão até chegarmos ao ponto de intervalo com confiança.

Mas, como sei quantos desvios devo andar?

Existem “números mágicos” que muita gente utiliza, sem saber de onde vem:

 

 

São os números correspondentes aos intervalos de confiança mais utilizados. Logo, se quisermos calcular o VaR com 95% de confiança, partimos da média e andamos 1,65 desvios para esquerda.

Selecionei esses graus de confiança, pois são os mais usados no mercado. No entanto, não precisamos ficar presos a esses intervalos. O Excel tem a função NORM.INV que, passando o intervalo de confiança, ela retorna o número de desvios necessários.

Portanto, os passos para calcular o VaR pelo método paramétrico normal no Excel são:

• Escolher o tamanho da amostra;
• Calcular os retornos na frequência desejada de horizonte de tempo;
• Estimar a média e o desvio padrão;
• Andar para esquerda um número de desvios relacionados ao grau de confiança, partindo da média.

O método paramétrico utilizando outras distribuições segue a mesma logica: Utilizar encaixar os retornos em uma distribuição, e usar os parâmetros dessa distribuição para chegar no ponto correspondente ao intervalo

Agora, é só baixar a planilha e ver na prática.

 

Planilha para Download