Matemática de Portfólio

Acesso ao Grupo Exclusivo de Telegram e aos cursos MF EXPERT => Click aqui
No artigo de hoje, vamos aprender como calcular o valor esperado e a volatilidade do portfólio e como implementar esses cálculos no Excel.
Retorno Portfólio
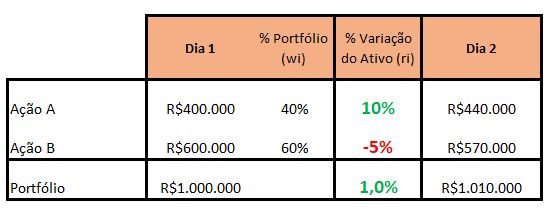
Para começar, vamos aprender a calcular o retorno do portfólio. Veja esse exemplo simples com duas ações.
O retorno do portfólio (+1%) pode ser calculado através da variação total do portfólio de um dia por outro.
Outra forma é calcular via a contribuição de cada ação para o resultado. Essa contribuição é o produto do peso do ativo no portfólio com a variação individual dele.
Por exemplo, se o ativo representar 10% do portfólio e ele subir 10% no dia, a contribuição deste ativo para a variação total do portfólio será 10%*10% = +1%. Ou Seja, se o resto todo do portfólio ficar parado, o portfólio subirá 1% no dia.
No exemplo anterior, a variação do portfólio pode ser calculada, então, por 40%*10% + 60%*-5% = +1%
Dessa forma, a fórmula geral do retorno do portfólio pode ser expressada por:
Valor Esperado do Portfólio
O valor esperado de um ativo é o quanto você espera que será a rentabilidade desse ativo em um certo período. Por exemplo, quanto você espera que a ação suba nos próximos meses.
Esse é o conceito!
O que causa muita confusão é que o valor esperado normalmente está associado a média de uma distribuição. Isso vem do conceito de valor esperado das aulas de probabilidade.
O problema de fazer isso em finanças (o que muitos livros fazem) é que você está assumindo que a média passada será igual a média futura. Se fosse verdade e tão simples assim, todos os estatísticos já estariam ricos!
Então, normalmente, o que os fundos fazem é uma análise detalhada de possíveis cenários e associam probabilidade a eles.
Por exemplo, tem 10% de chance de o ativo perder -10% em um ano; 15% de perder -5%; 30% de ganhar 10%; 25% de ganhar 15%; 20% de ganhar 20%
Nesse caso, o valor esperado seria igual a 9%!
10%*-10% + 15%*-5% + 30%*10% +25%*15% +20%*20% = 9%
Já percebemos, então, que o retorno do portfólio foi algo que já aconteceu e o valor esperado é algo que vai acontecer ainda. No entanto, ambos estão associados a retornos.
Dessa forma, o retorno esperado do portfólio segue a mesma linha:
Volatilidade de um Portfólio.
Vamos calcular agora a volatilidade (desvio padrão) para o portfólio com 2 ativos. Aqui vai entrar um pouco de matemática, mas nada muito complicado.
Logo, a volatilidade do portfólio é uma função do peso e da volatilidade de cada ativo e da correlação entre eles.
Lembrando que a correlação é uma medida estatística que indica o grau de como dois ativos se movem em relação um ao outro.
A correlação varia de -1 a 1.
Dois ativos com correlação 1, não necessariamente são iguais, mas se movem sempre na mesma direção. Já dois ativos com correlação -1, se movem sempre em direções opostas. Isso significa que, sempre que um ativo subir, o outro vai cair.
Efeito diversificação
Observando a fórmula da volatilidade, conseguimos entender o efeito da diversificação. No final deste artigo, há uma planilha para fazer as contas.
Vamos supor dois ativos. Ativo A com 10% de volatilidade e o ativo B também com 10% de volatilidade.
Se construirmos um portfólio com 50% de cada ativo, ao menos que a correlação entre eles seja igual a 1, a volatilidade do portfólio será menor que 10%!
COMO ASSIM??? Pego 2 ativos com volatilidade 10% e combino eles em um portfólio. A volatilidade do portfólio total será menor que 10%.
Isso é o efeito da diversificação. Como os ativos não tem correlação 1, eles não vão se mover necessariamente na mesma direção.
Exemplo, se a correlação entre eles for 0.5, a tendência é que se movam na mesma direção, mas há uma chance de se moverem em direções contrárias.
Então, se o ativo A cair, o ativo B pode subir e amenizar a perda do portfólio, por exemplo.
Por isso, a correlação negativa diminui ainda mais a volatilidade do portfólio, pois, aí sim, é de se esperar que se um ativo caia, o outro suba.
Em um portfólio de ações, por exemplo, se você adicionar uma posição em dólar (correlação negativa), a tendência é diminuir a volatilidade total do portfólio.
Caso N Ativos
Com 3 ativos, a volatilidade do portfólio fica em:
Já deu para perceber que, conforme vamos aumentando o número de ativos, a fórmula aumenta exponencialmente, né?
Para facilitar isso, conseguimos colocar a fórmula em uma forma matricial.
Se você entende de multiplicação de matrizes, faça o teste para dois ativos e verá que vai ficar exatamente igual a fórmula que calculamos.
Repare que, nessa fórmula, apareceu a matriz de correlação, algo muito usado em finanças. Nessa matriz, você pode ver a correlação de qualquer combinação de ativos do portfólio.
É importante observar essa matriz para encaixar no conceito para o conceito de diversificação do portfólio. Se você montar um portfólio com os ativos com correlações altas (acima de 0.8), você não terá um portfólio bem diversificado.
Cálculo no Excel
No final, temos a planilha para fazer todas essas contas.
São duas abas: uma para o caso de dois ativos que conseguimos fazer com o uso de uma fórmula e outra, para o caso de N ativos, que precisamos apelar para a fórmula matricial.
Você verá duas fórmulas complicadas: MMULT e TRANSPOSE. Aí há duas opções: tentar entender as fórmulas ou confiar que estamos calculando pela forma matricial.
Você vai reparar que antes e depois dessas fórmulas há um “{“. Eu já expliquei sobre esse tipo de fórmula aqui.
Planilha para Download


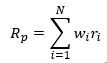
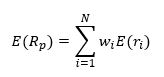

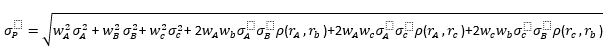
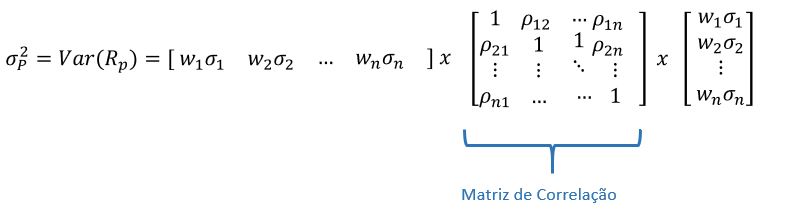
0 Comentários
What’s a floor ball with numerous pace called?