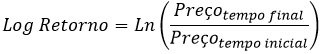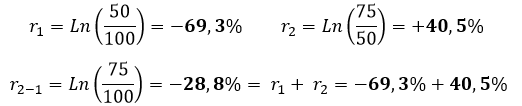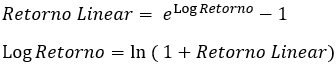Acesso ao Grupo Exclusivo de Telegram e aos cursos MF EXPERT => Click aqui

 

Introdução Artigo

 

No artigo de hoje, aprenderemos a diferença entre o retorno linear e o log retorno.

Também será abordado o conceito de fórmula de matriz (Array Formula) do Excel.

 

Introdução

 

Você vai ver em alguns posts deste blog o termo Log Retorno, muito usado em artigos acadêmicos, mas pouco utilizado na prática!

Antes de entrar no Log Retorno, vamos rever o retorno linear.

O retorno linear é o que estamos acostumados a usar no dia a dia. Quando falamos que uma ação caiu 10%, estamos nos referindo ao retorno linear.

O retorno linear entre o tempo inicial e o tempo final é dado por:

Já o Log Retorno neste mesmo período:

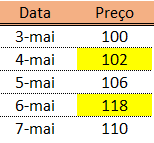
No exemplo abaixo, calculamos o retorno linear e Log Retorno entre o dia 4 (tempo inicial) e 6 (tempo final):

Mas por que usam o Log Retorno?

 

Vantagens do Log Retorno

 

Um exemplo clássico…

Se uma ação cai 50% e depois sobe 50%, de quanto foi a variação total no período?

Não é zero, né?

Vamos supor que a ação começa em 100.

Cai 50%… Passa a valer 50

Sobre 50%… Passa a valer 75.

De 100 para 75, ela cai então -25% no período inteiro.

Para compor esses dois períodos, considerando os retornos lineares, devemos usar a fórmula de juros compostos:

Para N dias, a fórmula geral é esse produtório:

É neste ponto que o Log Retorno apresenta a maior vantagem.

O Log Retorno Acumulado, é o somatório dos log retornos (r)! 

Essa propriedade simplifica muita conta, e é a principal razão de ele ser utilizado na maioria dos artigos acadêmicos.

No exemplo anterior:

Qual usar?

 

Uma dúvida geral é qual dos dois retornos usar. No cálculo da volatilidade aparece muito essa questão!

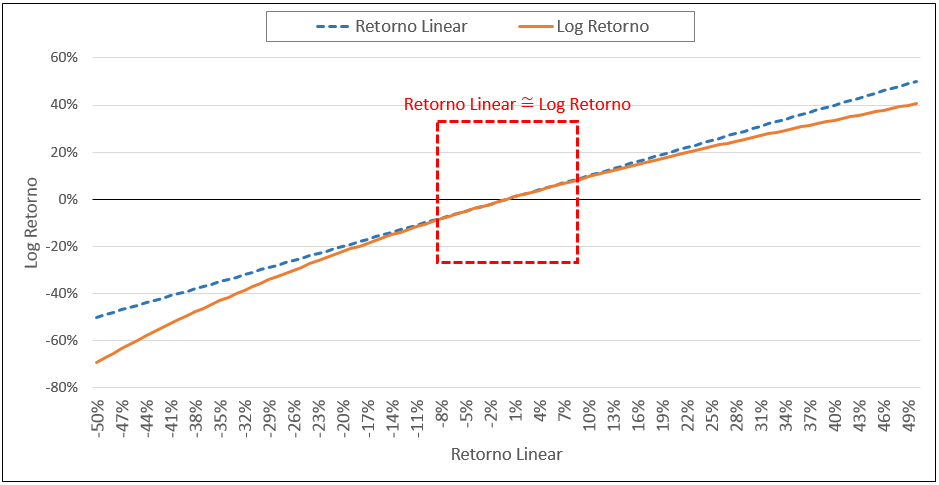
No entanto, quando estamos trabalhando com retornos diários, o retorno linear e o log retorno são aproximadamente iguais.

Portanto, na prática tanto faz!!

Retornos diários costumam ser pequenos. De uma ação, normalmente fica entre -5% a 5%.

Note a fórmula para converter um para o outro:

É fácil provar matematicamente que quanto menor o retorno em módulo, mais o retorno linear e o log retorno vão se tornando aproximadamente iguais!

 

 

Um fato que os artigos acadêmicos esquecem é que ninguém está acostumado com log-retorno.

Você pode até usar log-retorno para facilitar algumas contas, mas é importante, no final, apresentar o resultado em retorno linear.

Quando se fala que uma ação subiu 20%, na cabeça da maioria das pessoas, a ação passou de 100 para 120 e não de 100 para 122,1 (log retorno).

A ferramenta de hoje para download é mais uma ilustração desses cálculos de retornos.

No entanto, para o cálculo do retorno acumulado linear, há uma lição importante de excel: Trabalhar com fórmulas com Arrays.

Se seu interesse é entender os retornos, pode parar por aqui e fazer o donwload no final.

 

Fórmula de Matriz (Array Formula)

 

Esse é um tópico de Excel avançado.

Não é todo mundo que conhece essa funcionalidade. Ela vai aparecer algumas vezes neste blog.

Talvez você já deve ter visto algumas fórmulas com um “{“ no começo e no final , exemplo:

Essas fórmulas são geradas quando você clica na caixa da fórmula e pressiona ao mesmo tempo CTRL+SHIFT+ENTER.

Não adianta colocar o “{“ manualmente que não vai funcionar!

Essas são fórmulas matriciais. Não é tão intuitivo, e é um dos conceitos mais complicados do Excel.

Vou tentar deixar um pouco mais claro como funciona no exemplo a seguir.

Vamos supor que queremos calcular o retorno acumulado em um período, dado os retornos lineares.

 

 

Pela fórmula do retorno acumulado, eu preciso fazer o produtório de 1 + os retornos lineares.

Posso escrever manualmente:

 

 

Mas já viu que se aumentar muito a série, vai complicar. Vou ter que escrever uma fórmula gigante!

A segunda opção é criar uma coluna auxiliar de 1+Retorno Linear. E, depois, aplicar o produto direto dessa coluna.

 

Funciona, mas preciso criar uma coluna a mais para isso.

A opção mais simples é usando a fórmula matricial:

Note que se não fizer pressionando o CTRL+SHIFT+ENTER, não irá funcionar.

Sem a indicação da fórmula de array, o Excel tentará somar o  número 1 ao range C3:C6.

O que obviamente não será possível, porque você não pode somar número com range.

No entanto, com a indicação “{“ na fórmula, o Excel considera como fosse uma soma matricial.

Ele soma 1+ C3 e armazena no array…

Depois 1+C4 e armazena no array…

E assim vai até o final.

O que aconteceu foi que, no final das contas, foi criado na memória do Excel um array com esses dados.

Ou seja, para a memória do Excel, o que está dentro do PRODUCT é o Array {1,02;1,04;1,11;0,93}. Dessa forma, estou simulando o passo anterior sem precisar criar uma coluna extra.

Mais informação sobre fórmula de matriz, dá uma olhada nesse link da Microsoft.

 

Planilha para Download