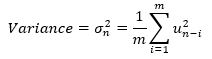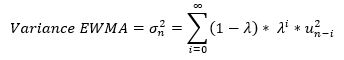Acesso ao Grupo Exclusivo de Telegram e aos cursos MF EXPERT => Click aqui

Introdução Artigo

No artigo de hoje, vamos aprender o que é e como calcular a volatilidade EWMA no Excel.

Volatilidade

Já vimos no artigo passado como se calcula a volatilidade da forma mais simples. No entanto, é importante entender dois conceitos diferentes.

Você pode calcular a volatilidade do que já ocorreu. Exemplo: Qual foi a volatilidade do fundo em 2017?

Nesses casos, você pode calcular a volatilidade da forma mais simples (desvio padrão).

A maior dificuldade, no entanto, é quando queremos prever a volatilidade futura. Exemplo: Qual será a volatilidade de ITUB4 nos próximos 3 meses?

Nesse contexto, calcular a volatilidade da forma simples, provavelmente, não trará as melhores previsões. É aí que entram métodos mais robustos, como o que vamos aprender agora, o EWMA.

Fatos Estilizados

Fatos estilizados são fatos observados empiricamente nos retornos financeiros. E sobre a volatilidade um fato é bem claro: a volatilidade não é constante no tempo.

Como teste, selecione os últimos 252 retornos diários do IBOVESPA, por exemplo. Agora calcule a volatilidade, considerando o período todo, e, também, em janelas móveis de 66 dias.

Ahh, não sabe aonde achar esses dados? Dê uma olhada nesse post aqui.

Muito provavelmente, você vai chegar a um gráfico assim:

Outro fato observado é a existência de clusters de volatilidade.

CLUSTERS DE VOLATILIDADE?!?

De maneira bem simplificada, clusters de volatilidade significa que um ativo tem uma volatilidade de longo prazo, mas, em certos momentos, pode ter períodos mais calmos ou mais agitados.

Logo, altos retornos são seguidos por altos retornos, seja o retorno positivo ou negativo. Assim como, é de se esperar que retornos menores sejam seguidos por retornos menores.

Os modelos para estimar a volatilidade querem incorporar nos cálculos esses fatos estilizados que são observados na prática. Tornando, assim, os modelos mais pertos do mundo real.

Dos mais utilizados, podemos destacar o GARCH e, justamente, o EWMA.

Modelo EWMA

Vamos pensar na fórmula da volatilidade simples, ou seja, a formula da variância. Só lembrando que a o desvio padrão é igual a raiz da variância.

Para simplificar, vamos supor que a média dos retornos diários (u) seja igual a zero (de fato, isso é observado empiricamente). Logo,

Note que todos os retornos têm o mesmo peso na conta. O retorno que aconteceu ontem vale o mesmo que o retorno que aconteceu há 252 dias.

O modelo de cálculo da volatilidade EWMA, Exponentially Weighted Moving Average, ou, em português, médias móveis exponencialmente ponderadas, tenta, então, dar maior peso aos retornos mais recentes.

Se pararmos para pensar, isso é justamente introduzir o conceito de cluster de volatilidade no modelo. Ou seja, altos retornos (em módulo) vão ajudar a aumentar a previsão de volatilidade, assim como, retornos menores vão ajudar a diminuir a volatilidade.

O modelo, então, introduz o parâmetro Lambda. Agora, observe a fórmula:

O lambda é justamente o parâmetro que faz essa média ponderada exponencial. Foi adotado um padrão de mercado de utilização do Lambda como 0,94.

Logo, como Lambda é menor que 1, quanto maior o i (retornos mais antigos) mais ele será penalizado.

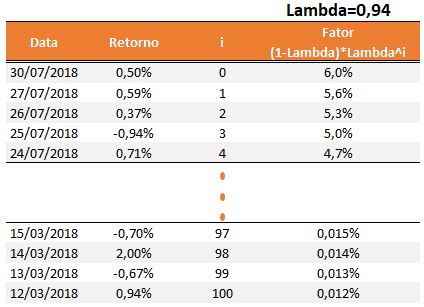
Sendo i=0 o retorno mais recente, agora observe a evolução do fator (1-Lambda)*Lambda^i, conforme os retornos vão ficando mais distantes.

Note, então, que quanto mais recente for o retorno, maior será o fator lambda, e conforme os retornos forem ficando mais antigos, menor será o peso na conta.

Note, também, que a fórmula é um somatório de 0 a infinito. Obviamente, você não precisa de infinitos retornos para calcular a volatilidade EWMA. Por volta do centésimo retorno, o fator lambda já fica quase irrelevante.

Portanto, pode usar os últimos 100 retornos para o primeiro cálculo.

Modelo EWMA Acumulado

O que aprendemos a fazer foi calcular a volatilidade EWMA considerando os 100 últimos retornos.

Outra vantagem da fórmula é que, calculada a volatilidade a primeira vez, podemos ir acumulando-a no tempo, de uma maneira bem simples, por essa fórmula.

Muita gente se confunde ao ver essa fórmula, porque não sabe de onde vem a primeira volatilidade. Você, então, precisa calcular a primeira volatilidade, usando os últimos 100 retornos como fizemos anteriormente.

EWMA no Excel

Na planilha Excel abaixo temos 3 sheets.

EWMA – Calcula a primeira volatilidade pelo método EWMA, utilizando os últimos 100 retornos.

EWMA_Rolling – Calcula a primeira volatilidade pelo método EWMA, utilizando os últimos 100 retornos. Depois, com essa volatilidade, inicial vamos calculando as volatilidades para as próximas datas, utilizando a fórmula:

EWMA_Rolling_Chart – Plota o gráfico das volatilidades, calculando em janelas móveis pelos métodos EWMA e pela volatilidade simples. É interessante observar como o método EWMA se adapta mais rápido às mudanças de mercado.

Planilha para Download